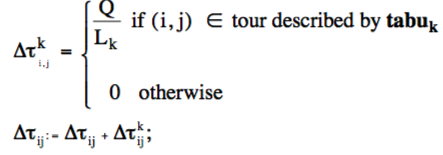Tìm kiếm trong không gian trạng thái và thuật toán Ant Colony Otimization

• Giới thiệu 

Trong loạt bài tìm kiếm trong không gian trạng thái ( về thuật toán Simulated Annealing có thể xem lại Simulated Annealing ), mình sẽ giới thiệu thêm về một giải thuật tìm kiếm cục bộ, đó là thuật toán Ant Colony Otimization. Mình vẫn tiếp tục dùng bài toán kinh điển để làm ví dụ, “Người bán hàng” – Bài toán tìm đường đi ngắn nhất đi qua tất cả các đỉnh, mỗi đỉnh đúng một lần, và trở về đỉnh xuất phát. 

• Tổng quan

Giống như thuật toán Simulated Annealing ( tôi thép ) dựa trên việc mô phỏng ký thuật “Tôi thép”, thì thuật toán Ant Colony Otimization cũng mô phỏng hoạt động tìm đường của đàn kiến. Kiến là một sinh vật mù, việc tìm đường đến nơi có thức ăn và trở về hoàn toàn dựa trên tín hiệu của bầy đàn đánh dấu trên đường đi ( gọi là pheromone trails ). Vậy tại sao đàn kiến luôn chọn được đường đi ngắn nhất? Thực ra ngay từ đầu, đàn kiến đi lung tung khắp nơi, và mỗi bước đi, chúng đều rải pheromone trên đường đi, và trên đường từ nguồn thức ăn về tổ, chúng đi qua đi lại nhiều lần, thì những lần tiếp theo di chuyển, những con kiến có xu hướng chọn cho mình con đường nơi có nồng độ pheromone  nhiều hơn (vì đường đó ngắn hơn, nên chúng đi tới nguồn thức ăn và trở về tổ nhanh hơn), sau một khoảng thời gian di chuyển, nồng độ pheromone bay hơi dần, cuối cùng chỉ còn lại con đường ngắn nhât vì nồng pheromone  được đàn kiến rải liên tục, còn những con đường xa hơn sẽ dần bay hơi hết pheromone, và sẽ bị đàn kiến bỏ qua.

• Mô tả chi tiết

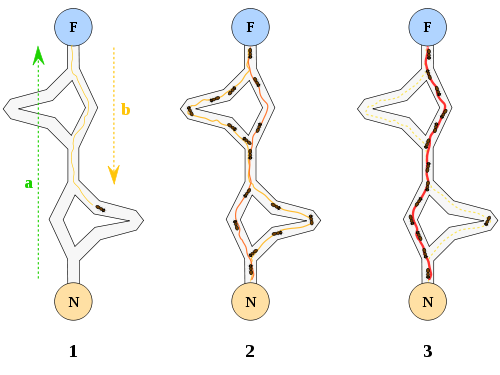
Dựa vào hình trên, giả sử đi từ N tới F và trở về có 4 con đường kiến có thể đi (H1). Tại thời gian đầu khi t = 0, đàn kiến bắt đầu toả ra tìm đường đi từ N tới F, thì con đường nào cũng sẽ có kiến đi qua (H2), và tại mỗi đường đi, kiến đều rải pheromone, nên lượng pheromone trên mỗi con đường là bằng nhau. Tại thời điểm t = 1, Có thể thấy rõ con đường ở chính giữa là ngắn nhất, nên khi còn kiến đầu tiên tìm tới F sẽ quay về lại N đầu tiên, sau khi về N, kiến sẽ lại tiếp tục di chuyển tới F, ở thời điểm này, cả 4 con đường đã bay hơi đi mất một lượng ρ nồng độ pheromone, nhưng tại con đường ngắn nhât, con những con kiến đã hoàn thành tour của mình sẽ tiếp tục rải thêm một lượng ∆τ, trong khi ở những con đường khác, những con kiến khác vẫn chưa hoàn thành tour của mình, có thể thấy rằng lượng pheromone đang dần có sự thay đổi về trọng số. Tại thời điển t = n, khi những con kiến khác về N tiếp tục cuộc hành trình, và khi lựa chọn con đường, chúng sẽ có xu hướng chọn cho mình con đường có nồng độ pheromone cao hơn, và con đường ngắn nhât chính là con đường được đàn kiến đi qua nhiều nhất (H3).

Giống với thuật toán SA (Simulated Annealing) thì thuật toán ACO (Ant Colony Otimization) là một loạt thuật toán tối ưu hoá ngẫu nhiên tổ hợp (stochastic combinatorial optimization) _ hay có thể nói đơn giản là việc tìm ra cấu hình “chấp nhận được” bằng phương pháp “random”. Trong những bài toán này thường hay đề cập đến một hàm heuristic, hàm này như là trái tim của thuật toán, việc lựa chọn ra cấu hình tiếp theo như thế nào phụ thuộc hoàn toàn vào heuristic. 

• Thuật toán

Mình sẽ bắt đầu mô tả thuật toán như sau:

1. Khởi tạo:
Đặt t:=0                                               // t thời gian đếm
Đặt NC:=0                                              // NC số chu trình
Với mỗi cạnh (i,j) khởi tạo giá trị τ(ij)(t) = c cường độ bào mòn ∆τ(ij)= 0 và đặt m con kiến trên n nút

2. Đặt s:=1                                            // s là chỉ mục trên danh sách tabu 
                                                       // (danh sách tabu để đánh dấu, thành phố nào đã được đi qua)
For k:=1 to m do
Đặt thành phố xuất phát của con kiến thứ k vào danh sách tabu_k(s)

3. Lặp cho đến khi danh sách đầy                       // bước này sẽ lặp khoảng (n-1) lần
Set s:=s+1 
For k:=1 to m do
Chọn thành phố thứ  j để di chuyển tới, với xác suất p(t) được cho bởi biểu thức:

(Hàm tính xác suất di chuyển trên cạnh (i,j) có thể coi như hàm heuristic của thuật toán ACO. 
Trong biểu thức trên có thể hiểu thành phố thứ j của con kiến thứ k ∈ allowed là những thành phố chưa được tới thăm. 
α và β là những tham số kiểm soát ta đặt từ ban đầu. Trong biểu thức trên τij(t) là tổng số lượng pheromone được rải 
trên cạnh ij tại thời điểm t, τik(t) là tổng số lượng pheromone được rải trên cạnh ik tại thời điểm t của tất cả 
những thành phố chưa được thăm. ηij = 1/dij _ dij là chiều dài cạnh ij. 
Có thể hiểu, xác suất p phụ thuộc vào 2 yếu tố, nếu như τij(t) cao  lượng pheromone được rải trên cạnh ij nhiều hơn, 
và thành phố thứ j gần thành phố i thì ηij càng lớn => p cũng càng lớn )

// tại thời điểm t con kiến thứ k trên thành phố thứ i sẽ : i = tabu_k(s-1)
Di chuyển con kiến thứ k tới thành phố  j. Thêm thành phố j vào tabu_k(s)

4. For k:=1 to m do
Di chuyển con kiến thứ ktabu_k(n) về tabuk(1)
Tính toán độ dài của tour  Lk bởi con kiến thứ k và cập nhật đường đi ngắn nhất tìm đườngVới mỗi cạnh (i,j)For k:=1 to m do

(τij được cập nhật lại sau mỗi chu trình, với mỗi con kiến k sẽ rải lên cạnh ij một lượng 
pheromone là Q/Lk _ Q là một hằng số cho trước, Lk là độ dài của tour. 
Lượng pheromone được tính bằng số lượng pheromone  của tất cả những con kiến đi qua cạnh ij)

5. Với mỗi cạnh (i,j) tính toán lại nồng độ pheromone theo công thức τij(t+n)=ρ.τij(t)+∆τij
Cập nhật t:=t+n
Cập nhật NC:=NC+1
Với mỗi cạnh (i,j) đặt ∆τij:=0

6. If (NC < NCmax) và  (không phải stagnation behavior)   // stagnation behavior là khi thuật toán đã ở trạng thái không thể thực 
                                                          // hiện tiếp được nữa, ở đây là tất cả đàn kiến đang đi trên cùng một đường rồi
       Làm rỗng tất cả danh sách tabu và quay lại bước 2
   Else đưa ra con đường ngắn nhất và kết thúc

Link tham khảo: [1] M. Dorigo, The Ant System: Optimization by a colony of cooperating agents ftp://iridia.ulb.ac.be/pub/mdorigo/journals/IJ.10-SMC96.pdf

• Source code

// Store in probs array the probability of moving to each town
// [1] describes how these are calculated.
// In short: ants like to follow stronger and shorter trails more.
private void probTo(Ant ant) {
    int i = ant.tour[currentIndex];

    double denom = 0.0;
    for (int l = 0; l < n; l++)
        if (!ant.visited(l))
            denom += pow(trails[i][l], alpha)
                    * pow(1.0 / graph[i][l], beta);


    for (int j = 0; j < n; j++) {
        if (ant.visited(j)) {
            probs[j] = 0.0;
        } else {
            double numerator = pow(trails[i][j], alpha)
                    * pow(1.0 / graph[i][j], beta);
            probs[j] = numerator / denom;
        }
    }

}

// Given an ant select the next town based on the probabilities
// we assign to each town. With pr probability chooses
// totally randomly (taking into account tabu list).
private int selectNextTown(Ant ant) {
    // sometimes just randomly select
    if (rand.nextDouble() < pr) {
        int t = rand.nextInt(n - currentIndex); // random town
        int j = -1;
        for (int i = 0; i < n; i++) {
            if (!ant.visited(i))
                j++;
            if (j == t)
                return i;
        }

    }
    // calculate probabilities for each town (stored in probs)
    probTo(ant);
    // randomly select according to probs
    double r = rand.nextDouble();
    double tot = 0;
    for (int i = 0; i < n; i++) {
        tot += probs[i];
        if (tot >= r)
            return i;
    }

    throw new RuntimeException("Not supposed to get here.");
}

// Update trails based on ants tours
private void updateTrails() {
    // evaporation
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            trails[i][j] *= evaporation;

    // each ants contribution
    for (Ant a : ants) {
        double contribution = Q / a.tourLength();
        for (int i = 0; i < n - 1; i++) {
            trails[a.tour[i]][a.tour[i + 1]] += contribution;
        }
        trails[a.tour[n - 1]][a.tour[0]] += contribution;
    }
}

// Choose the next town for all ants
private void moveAnts() {
    // each ant follows trails...
    while (currentIndex < n - 1) {
        for (Ant a : ants)
            a.visitTown(selectNextTown(a));
        currentIndex++;
    }
}